简单题
414. 第三大的数
给你一个非空数组,返回此数组中 第三大的数 。如果不存在,则返回数组中最大的数。
示例 1:
- 输入: [3, 2, 1]
- 输出: 1
- 解释: 第三大的数是 1 。
示例 2:
- 输入: [1, 2]
- 输出: 2
- 解释: 第三大的数不存在, 所以返回最大的数 2 。
示例 3:
- 输入: [2, 2, 3, 1]
- 输出: 1
- 解释: 注意,要求返回第三大的数,是指在所有不同数字中排第三大的数。此例中存在两个值为 2 的数,它们都排第二。在所有不同数字中排第三大的数为 1 。
参考代码
| |
主要逻辑
初始化:
- 使用长整型的最小值
LONG_LONG_MIN初始化三个变量:maxNum、midNum和minNum,分别代表当前的最大值、中间值和最小值。
- 使用长整型的最小值
遍历数组:
- 使用范围基 for 循环遍历
nums数组中的每一个数字n。 - 更新条件:
- 如果当前数字
n大于maxNum,则更新最大值、以及中间值和最小值:- 中间值
midNum变为之前的最大值maxNum。 - 最小值
minNum变为之前的中间值midNum。 - 最大值
maxNum更新为当前数字n。
- 中间值
- 如果当前数字
n在最大值和中间值之间,更新中间值和最小值:- 最小值
minNum变为之前的中间值midNum。 - 中间值
midNum更新为当前数字n。
- 最小值
- 如果当前数字
n在中间值和最小值之间,更新最小值:- 最小值
minNum更新为当前数字n。
- 最小值
- 如果当前数字
- 使用范围基 for 循环遍历
返回结果:
- 遍历结束后,检查
minNum是否仍为LONG_LONG_MIN:- 如果是,则表示数组中不存在第三大的数,返回
maxNum。 - 否则返回
minNum,即第三大的数字。
- 如果是,则表示数组中不存在第三大的数,返回
- 遍历结束后,检查
605. 种花问题
假设有一个很长的花坛,一部分地块种植了花,另一部分却没有。可是,花不能种植在相邻的地块上,它们会争夺水源,两者都会死去。
给你一个整数数组 flowerbed 表示花坛,由若干 0 和 1 组成,其中 0 表示没种植花,1 表示种植了花。另有一个数 n ,能否在不打破种植规则的情况下种入 n 朵花?能则返回 true ,不能则返回 false 。
示例 1:
- 输入: flowerbed = [1,0,0,0,1], n = 1
- 输出: true
示例 2:
- 输入: flowerbed = [1,0,0,0,1], n = 2
- 输出: false
参考代码
第一版
| |
实现思路
变量定义
rest: 用于记录可以种植的花的数量。
遍历花坛数组
- 使用一个for循环遍历
flowerbed数组。 - 如果当前位置已经种植了花(
flowerbed[i] == 1),则跳过下一个位置(++i),继续下一个循环。 - 如果当前位置没有种植花(
flowerbed[i] == 0),则检测相邻位置:- 最后一个位置处理:若是最后一个位置,直接增加
rest并退出循环。 - 相邻位置检查:若下一个位置也是空的(
flowerbed[i + 1] == 0),可以在当前位置种植一朵花并记录已种植数量,通过将flowerbed[i]设置为1来进行标记。
- 最后一个位置处理:若是最后一个位置,直接增加
- 如果不满足相邻位置的条件,则继续遍历。
- 使用一个for循环遍历
返回结果
- 最终,通过比较
rest和n来判断是否能成功种植所需数量的花,如果rest >= n,返回true,否则返回false。
- 最终,通过比较
第一版修改
第一版代码简化,但是效率低了
| |
第二版
| |
实现步骤
初始化变量:
rest: 用于记录可以种植的花的数量,初始值为0。
简化边界判断:
- 在flowerbed数组的开头插入一个0,表示花坛开始位置。
- 在数组末尾增加一个0,表示花坛结束位置。这样处理简化了后续的边界判断。
遍历花坛:
- 从第二个位置(
i = 1)开始遍历到倒数第二个位置(i < flowerbed.size() - 1): - 检查当前地块、左边地块和右边地块是否都为0。
- 如果满足条件,则在当前地块种一朵花,更新
flowerbed[i]为1,并增加rest的值。
- 从第二个位置(
返回结果:
- 在遍历完成后,判断
rest是否大于或等于n。 - 如果
rest >= n,返回true,否则返回false。
- 在遍历完成后,判断
628. 三个数的最大乘积
给你一个整型数组 nums ,在数组中找出由三个数组成的最大乘积,并输出这个乘积。
示例 1:
- 输入: nums = [1,2,3]
- 输出: 6
示例 2:
- 输入: nums = [1,2,3,4]
- 输出: 24
示例 3:
- 输入: nums = [-1,-2,-3]
- 输出: -6
参考代码
| |
实现步骤
参数与返回值:
- 输入:一个整型数组
nums,长度大于等于3。 - 输出:返回三个数的最大乘积。
- 输入:一个整型数组
数组排序:
- 使用
sort函数对数组进行排序,以便后续容易访问最大和最小的元素。
- 使用
基本条件判断:
- 如果数组的最小值大于等于0(数组全为非负数),或者数组的最大值为负数,直接返回三个最大的数的乘积。
初始化变量:
firstNum、secondNum、thirdNum:用于存储当前计算的最大的三个数。Max:初始化为INT_MIN,用于记录最大乘积。temp:暂时存储当前计算的乘积。n:统计负数的数量。
统计负数:
- 使用
while循环遍历数组,统计负数的数量,存储到n中。
- 使用
分割负数与正数:
- 根据统计结果,将负数和正数分别存储到两个不同的向量
fushu(负数部分)和zhengshu(正数部分)。
- 根据统计结果,将负数和正数分别存储到两个不同的向量
计算负数与正数组合的乘积:
- 如果负数部分包含两个或更多的负数,则计算两个负数与一个最大正数的乘积,并更新
Max。
- 如果负数部分包含两个或更多的负数,则计算两个负数与一个最大正数的乘积,并更新
遍历计算:
- 从数组末尾开始,遍历计算三个最大的数的乘积,并更新
Max。
- 从数组末尾开始,遍历计算三个最大的数的乘积,并更新
返回结果:
- 返回记录的最大乘积
Max。
- 返回记录的最大乘积
643. 子数组最大平均数 I
给你一个由 n 个元素组成的整数数组 nums 和一个整数 k 。
请你找出平均数最大且 长度为 k 的连续子数组,并输出该最大平均数。
任何误差小于 10-5 的答案都将被视为正确答案。
示例 1:
- 输入: nums = [1,12,-5,-6,50,3], k = 4
- 输出: 12.75
- 解释: 最大平均数 (12-5-6+50)/4 = 51/4 = 12.75
示例 2:
- 输入: nums = [5], k = 1
- 输出: 5.00000
参考代码
| |
主要逻辑
特殊情况处理:
- 当数组只有一个元素时,直接返回该元素的值。
- 当
k为 1 时,遍历数组找到最大元素并返回。
初始和计算:
- 使用
accumulate函数计算初始的前k个元素的累加和,并将其转换为double类型以便进行后续操作。
- 使用
滑动窗口遍历:
- 使用循环检查所有可能的连续子数组。通过滑动窗口的思想,当遇到新的元素时,判断是否需要更新当前的最大和。
- 如果发现的新子数组的和大于之前计算的最大和,则更新最大和。
返回最大平均数:
- 最后返回找到的最大和除以
k,以获得最大平均数。
- 最后返回找到的最大和除以
674. 最长连续递增序列
给定一个未经排序的整数数组,找到最长且 连续递增的子序列,并返回该序列的长度。
连续递增的子序列 可以由两个下标 l 和 r(l < r)确定,如果对于每个 l <= i < r,都有 nums[i] < nums[i + 1] ,那么子序列 [nums[l], nums[l + 1], …, nums[r - 1], nums[r]] 就是连续递增子序列。
示例 1:
- 输入: nums = [1,3,5,4,7]
- 输出: 3
- 解释: 最长连续递增序列是 [1,3,5] , 长度为3。尽管 [1,3,5,7] 也是升序的子序列, 但它不是连续的,因为 5 和 7 在原数组里被 4 隔开。
示例 2:
- 输入: nums = [2,2,2,2,2]
- 输出: 1
- 解释: 最长连续递增序列是 [2] , 长度为1。
参考代码
| |
代码逻辑
初始化变量:
len:用来记录当前找到的最长连续递增子序列的长度,初始值为1。temp:临时变量,用于存储当前递增子序列的长度,初始值也为1。
遍历数组:
- 使用
for循环遍历数组,范围是从 0 到nums.size() - 1,避免数组越界。
- 使用
判断递增关系:
- 在循环中,通过比较当前元素和下一个元素的大小来判断是否为递增关系:
- 如果当前元素小于下一个元素,则递增长度
temp加1。 - 如果
temp大于len,则更新len为temp,记录新的最长长度。 - 如果当前元素不小于下一个元素,说明递增关系断裂,将
temp重置为1,表示新的递增子序列开始。
- 如果当前元素小于下一个元素,则递增长度
- 在循环中,通过比较当前元素和下一个元素的大小来判断是否为递增关系:
返回结果:
- 循环结束后,检查
len是否仍为1(说明没有找到更长的连续递增子序列),如果是,则返回temp的值;否则,返回len的值。
- 循环结束后,检查
697. 数组的度
给定一个非空且只包含非负数的整数数组 nums,数组的 度 的定义是指数组里任一元素出现频数的最大值。
你的任务是在 nums 中找到与 nums 拥有相同大小的度的最短连续子数组,返回其长度。
示例 1:
- 输入: nums = [1,2,2,3,1]
- 输出: 2
- 解释: 输入数组的度是 2 ,因为元素 1 和 2 的出现频数最大,均为 2 。 连续子数组里面拥有相同度的有如下所示: [1, 2, 2, 3, 1], [1, 2, 2, 3], [2, 2, 3, 1], [1, 2, 2], [2, 2, 3], [2, 2] 最短连续子数组 [2, 2] 的长度为 2 ,所以返回 2 。
示例 2:
- 输入: nums = [1,2,2,3,1,4,2]
- 输出: 6
- 解释: 数组的度是 3 ,因为元素 2 重复出现 3 次。 所以 [2,2,3,1,4,2] 是最短子数组,因此返回 6 。
参考代码
| |
函数逻辑
定义变量:
arr[50000]用于存储数组中每个数字的出现频率。du记录最大频率(数组的度)。minlen初始为最大整数,用于存储最短子数组的长度。
统计频率:
- 遍历
nums数组,对每个数字进行计数,更新arr数组。
- 遍历
寻找最大频率和候选数字:
- 遍历频率数组
arr:- 如果当前出现次数等于
du,则将该数字添加到候选数组dus。 - 如果当前次数超过
du,更新du为当前次数,并清空dus,将当前数字加入。
- 如果当前出现次数等于
- 遍历频率数组
计算候选数字的连续子数组长度:
- 遍历候选数组
dus,对每个候选数字进行以下操作:- 初始化
first为 -1,用于记录该数字第一次出现的位置。 - 遍历
nums,找到该候选数字的出现次数,当找到足够的次数时停止。 - 计算当前连续子数组的长度并存储到
lens数组。
- 初始化
- 遍历候选数组
寻找最短子数组长度:
- 遍历存储的各个长度
lens,找到最小的子数组长度minlen。
- 遍历存储的各个长度
返回结果:
- 返回最短长度
minlen。
- 返回最短长度
717. 1 比特与 2 比特字符
有两种特殊字符:
- 第一种字符可以用一比特
0表示 - 第二种字符可以用两比特(
10或11)表示
给你一个以 0 结尾的二进制数组 bits ,如果最后一个字符必须是一个一比特字符,则返回 true 。
示例 1:
- 输入: bits = [1, 0, 0]
- 输出: true
- 解释: 唯一的解码方式是将其解析为一个两比特字符和一个一比特字符。 所以最后一个字符是一比特字符。
示例 2:
- 输入: bits = [1,1,1,0]
- 输出: false
- 解释: 唯一的解码方式是将其解析为两比特字符和两比特字符。 所以最后一个字符不是一比特字符。
参考代码
| |
代码详细分析
基本情况处理:
- 如果
bits数组的长度为1且其唯一元素为0,直接返回true,说明最后一个字符是一个一比特字符。
- 如果
准备工作:
- 在数组的开头插入一个0,这样可以简化后续处理,使得在倒序遍历时方便判断。
逆向遍历:
- 从倒数第二个元素开始向前遍历,寻找一比特字符的起始点(即值为0的元素)。
- 一旦找到0,计算当前元素到最后一位的距离,如果这个距离减1后是偶数,说明最后一个字符是一个一比特字符,标志变量
flag设置为true。
循环退出:
- 找到第一个0后退出循环,避免不必要的遍历。
返回结果:
- 最后返回
flag的值,即判断结果。
- 最后返回
724. 寻找数组的中心下标
给你一个整数数组 nums ,请计算数组的 中心下标 。
数组 中心下标 是数组的一个下标,其左侧所有元素相加的和等于右侧所有元素相加的和。
如果中心下标位于数组最左端,那么左侧数之和视为 0 ,因为在下标的左侧不存在元素。这一点对于中心下标位于数组最右端同样适用。
如果数组有多个中心下标,应该返回 最靠近左边 的那一个。如果数组不存在中心下标,返回 -1 。
示例 1:
- 输入: nums = [1, 7, 3, 6, 5, 6]
- 输出: 3
- 解释: 中心下标是 3 。左侧数之和 sum = nums[0] + nums[1] + nums[2] = 1 + 7 + 3 = 11 ,右侧数之和 sum = nums[4] + nums[5] = 5 + 6 = 11 ,二者相等。
示例 2:
- 输入: nums = [1, 2, 3]
- 输出: -1
- 解释: 数组中不存在满足此条件的中心下标。
示例 3:
- 输入: nums = [2, 1, -1]
- 输出: 0
- 解释: 中心下标是 0 。左侧数之和 sum = 0 ,(下标 0 左侧不存在元素),右侧数之和 sum = nums[1] + nums[2] = 1 + -1 = 0 。
参考代码
| |
核心逻辑
初始化:
result初始化为 -1,表示默认没有找到任何中心下标。leftSum和rightSum分别用于计算左侧和右侧的元素和。
遍历数组:
- 使用一个反向循环,从数组的最后一个元素开始向前遍历。
- 对于每一个元素,计算其左侧和右侧的元素和。
计算和:
- 如果当前下标为 0,则左侧元素和视为 0;如果当前下标为数组的最后一个索引,则右侧元素和视为 0。
- 使用
accumulate函数计算指定范围内元素的和。
中心下标判定:
- 判断左侧和是否等于右侧和,如果相等,则更新
result为当前下标。
- 判断左侧和是否等于右侧和,如果相等,则更新
返回结果:
- 遍历完成后返回
result,即找到的中心下标或者 -1。
- 遍历完成后返回
747. 至少是其他数字两倍的最大数
给你一个整数数组 nums ,其中总是存在 唯一的 一个最大整数 。
请你找出数组中的最大元素并检查它是否 至少是数组中每个其他数字的两倍 。如果是,则返回 最大元素的下标 ,否则返回 -1 。
示例 1:
- 输入: nums = [3,6,1,0]
- 输出: 1
- 解释: 6是最大的整数,对于数组中的其他整数,6至少是数组中其他元素的两倍。6的下标是1,所以返回 1 。
示例 2:
- 输入: nums = [1,2,3,4]
- 输出: -1
- 解释: 4 没有超过 3 的两倍大,所以返回 -1 。
参考代码
| |
实现步骤
创建副本:使用
vector<int> temp = nums;创建原始数组的副本,以便后续查找最大元素的下标时不受排序的影响。排序:使用
sort(nums.begin(), nums.end());对数组进行排序,以便可以快速找到最大元素及其相邻元素(第二大元素)。条件判断:
- 检查最大元素是否至少是第二大元素的两倍,使用条件
if (nums[nums.size() - 1] / 2 >= nums[nums.size() - 2])实现。 - 如果条件满足,继续下一步;否则返回 -1。
- 检查最大元素是否至少是第二大元素的两倍,使用条件
查找下标:
- 使用循环遍历副本数组
temp,找到最大元素并返回其下标。 - 利用条件
if (max == temp[i])判断当前元素是否为最大元素。
- 使用循环遍历副本数组
返回结果:
- 如果找到了符合条件的最大元素,返回它的下标;如果没有,返回 -1。
830 最大分组的位置
在一个由小写字母构成的字符串 s 中,包含由一些连续的相同字符所构成的分组。
例如,在字符串 s = "abbxxxxzyy" 中,就含有 "a", "bb", "xxxx", "z" 和 "yy" 这样的一些分组。
分组可以用区间 [start, end] 表示,其中 start 和 end 分别表示该分组的起始和终止位置的下标。上例中的 "xxxx" 分组用区间表示为 [3,6] 。
我们称所有包含大于或等于三个连续字符的分组为 较大分组 。
找到每一个 较大分组 的区间,按起始位置下标递增顺序排序后,返回结果。
示例 1:
- 输入: s = “abbxxxxzzy”
- 输出: [ [3,6] ]
- 解释: “xxxx” 是一个起始于 3 且终止于 6 的较大分组。
示例 2:
- 输入: s = “abc”
- 输出: []
- 解释: “a”,“b” 和 “c” 均不是符合要求的较大分组。
示例 3:
- 输入: s = “abcdddeeeeaabbbcd”
- 输出: [ [3,5],[6,9],[12,14] ]
- 解释: 较大分组为 “ddd”, “eeee” 和 “bbb”
示例 4:
- 输入: s = “aba”
- 输出: []
参考代码
| |
关键步骤
参数与返回值:
- 输入:一个字符串
s。 - 输出:一个二维向量
vector<vector<int>>,其中每个子向量包含一个较大分组的起始和结束位置。
- 输入:一个字符串
处理边界条件:
- 如果字符串长度小于 3,直接返回空的结果。
- 在字符串末尾附加一个不会与原字符串重复的字符(如
'0'),以便在遍历时能够完整处理最后一个分组。
变量定义:
temp:用于临时存储当前较大分组的起始和结束位置。result:最终存储所有较大分组的结果。
遍历字符串:
- 使用
for循环遍历字符串的每个字符。 - 如果当前字符与
temp中的起始字符不相同,表示一个分组结束,更新temp和result,然后清空temp。 - 如果当前字符与
temp中的起始字符相同,则跳过当前迭代。 - 检查当前字符与其后两个字符是否相同,如果相同,记录起始位置并调整迭代变量
i,以跳过连续字符。
- 使用
返回结果:
- 函数返回所有找到的较大分组的起始和结束位置。
888. 公平的糖果交换
爱丽丝和鲍勃拥有不同总数量的糖果。给你两个数组 aliceSizes 和 bobSizes ,aliceSizes[i] 是爱丽丝拥有的第 i 盒糖果中的糖果数量,bobSizes[j] 是鲍勃拥有的第 j 盒糖果中的糖果数量。
两人想要互相交换一盒糖果,这样在交换之后,他们就可以拥有相同总数量的糖果。一个人拥有的糖果总数量是他们每盒糖果数量的总和。
返回一个整数数组 answer,其中 answer[0] 是爱丽丝必须交换的糖果盒中的糖果的数目,answer[1] 是鲍勃必须交换的糖果盒中的糖果的数目。如果存在多个答案,你可以返回其中 任何一个 。题目测试用例保证存在与输入对应的答案。
示例 1:
- 输入: aliceSizes = [1,1], bobSizes = [2,2]
- 输出: [1,2]
示例 2:
- 输入: aliceSizes = [1,2], bobSizes = [2,3]
- 输出: [1,2]
示例 3:
- 输入: aliceSizes = [2], bobSizes = [1,3]
- 输出: [2,3]
示例 4:
- 输入: aliceSizes = [1,2,5], bobSizes = [2,4]
- 输出: [5,4]
参考代码
| |
主要步骤
计算糖果总量:
sumA: 通过accumulate函数计算爱丽丝的糖果总和。sumB: 计算鲍勃的糖果总和。
计算交换所需的糖果数量:
Cab: 计算爱丽丝与鲍勃糖果总量的差的一半,公式为(sumB - sumA) / 2。这是为了找出爱丽丝需要给鲍勃的糖果数量。
寻找交换的个体:
- 通过两层循环遍历爱丽丝和鲍勃的糖果盒子。
- 对于每一盒爱丽丝的糖果,计算
x = m - Cab,表示爱丽丝需要交换的糖果数量。 - 内层循环遍历鲍勃的糖果盒子,检查爱丽丝要交换的数量是否与鲍勃的某盒糖果相等。
返回结果:
- 一旦找到了可以交换的糖果数量,即
x == n,就返回爱丽丝和鲍勃需要交换的糖果数量。
- 一旦找到了可以交换的糖果数量,即
914. 卡牌分组
给定一副牌,每张牌上都写着一个整数。
此时,你需要选定一个数字 X,使我们可以将整副牌按下述规则分成 1 组或更多组:
- 每组都有
X张牌。 - 组内所有的牌上都写着相同的整数。
仅当你可选的 X >= 2 时返回 true。
示例 1:
- 输入: deck = [1,2,3,4,4,3,2,1]
- 输出: true
- 解释: 可行的分组是 [1,1],[2,2],[3,3],[4,4]
示例 2:
- 输入: deck = [1,1,1,2,2,2,3,3]
- 输出: false
- 解释: 没有满足要求的分组。
参考代码
| |
实现步骤
统计出现次数:
- 创建一个大小为10001的数组
arr用于记录每个数字在牌组中出现的次数。 - 遍历
deck,对每个数字进行计数。
- 创建一个大小为10001的数组
排序:
- 对计数后的数组
arr进行排序,从小到大。
- 对计数后的数组
找到第一个非零出现次数:
- 通过循环,跳过数组中值为0的元素,找到第一个非零的出现次数。
计算最大公约数:
- 从第一个非零出现次数开始,利用辗转相除法计算所有出现次数的最大公约数。
- 初始最大公约数为第一个非零出现次数,从第二个出现次数开始与当前最大公约数进行计算,直到遍历完整个数组。
检查最大公约数:
- 最后判断计算出的最大公约数
result是否大于等于2,返回相应的布尔值。
- 最后判断计算出的最大公约数
941. 有效的山脉数组
给定一个整数数组 arr,如果它是有效的山脉数组就返回 true,否则返回 false。
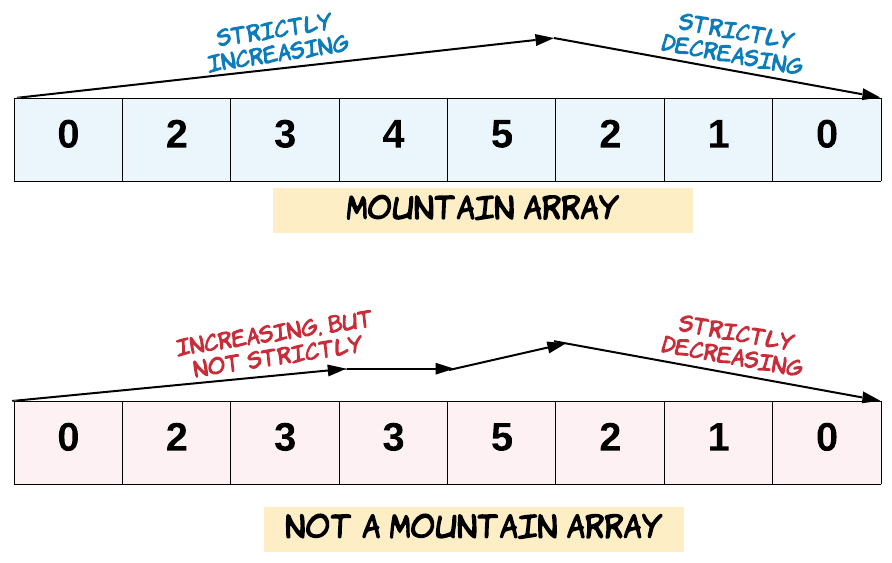
让我们回顾一下,如果 arr 满足下述条件,那么它是一个山脉数组:
arr.length >= 3- 在
0 < i < arr.length - 1条件下,存在i使得:arr[0] < arr[1] < … arr[i-1] < arr[i]arr[i] > arr[i+1] > … > arr[arr.length - 1]
示例 1:
- 输入: arr = [2,1]
- 输出: false
示例 2:
- 输入: arr = [3,5,5]
- 输出: false
示例 3:
- 输入: arr = [0,3,2,1]
- 输出: true
参考代码
| |
实现思路
边界检查:
- 首先检查数组的大小是否小于 3。如果小于,则直接返回
false,因为不能形成山脉。
- 首先检查数组的大小是否小于 3。如果小于,则直接返回
指针初始化:
- 使用两个指针
i和j。i从数组的开头开始前进。j从数组的末尾开始后退。
- 使用两个指针
查找递增部分:
- 通过
while循环,从前往后查找,直到数组元素不再递增。循环条件为arr[i + 1] > arr[i],表示当前元素小于下一个元素。
- 通过
查找递减部分:
- 通过另一个
while循环,从后往前查找,直到数组元素不再递减。循环条件为arr[j - 1] > arr[j]。
- 通过另一个
指针相遇检查:
- 最后,检查两个指针
i和j是否相遇,并且指针的位置是否在有效范围内(即i不能是最后一个元素,j不能是第一个元素)。
- 最后,检查两个指针
989. 数组形式的整数加法
整数的 数组形式 num 是按照从左到右的顺序表示其数字的数组。
- 例如,对于
num = 1321,数组形式是[1,3,2,1]。
给定 num ,整数的 数组形式 ,和整数 k ,返回 整数 num + k 的 数组形式 。
示例 1:
- 输入: num = [1,2,0,0], k = 34
- 输出: [1,2,3,4]
- 解释: 1200 + 34 = 1234
示例 2:
- 输入: num = [2,7,4], k = 181
- 输出: [4,5,5]
- 解释: 274 + 181 = 455
示例 3:
- 输入: num = [2,1,5], k = 806
- 输出: [1,0,2,1]
- 解释: 215 + 806 = 1021
参考代码
| |
3. 关键步骤解析
初始化:
- 创建一个空的结果数组
res用于存储结果。 - 使用
digit变量存储当前需要处理的数字,sum用于存储当前两位相加的结果。
- 创建一个空的结果数组
从后向前遍历:
- 使用一个 for 循环从
num的末尾开始遍历每一位数字。 - 在每一次迭代中,获取
k的最后一位 (digit = k % 10),并与当前位num[i]相加得到sum。 - 更新
k以去除已经计算的最后一位 (k /= 10)。
- 使用一个 for 循环从
处理进位:
- 如果
sum大于 9,表示需要进位。进位的处理方式是将k加 1,并更新sum保留当前位的数字(sum = sum % 10)。
- 如果
添加结果:
- 将计算得到的
sum添加到结果数组res中。
- 将计算得到的
处理剩余的
k:- 如果在遍历结束后,
k仍然大于 0,则继续处理k的剩余位,将每一位依次添加到结果数组中。
- 如果在遍历结束后,
反转结果数组:
- 最后将结果数组反转,以确保返回的数字顺序是正确的。
1128. 等价多米诺骨牌对的数量
给你一组多米诺骨牌 dominoes 。
形式上,dominoes[i] = [a, b] 与 dominoes[j] = [c, d] 等价 当且仅当 (a == c 且 b == d) 或者 (a == d 且 b == c) 。即一张骨牌可以通过旋转 0 度或 180 度得到另一张多米诺骨牌。
在 0 <= i < j < dominoes.length 的前提下,找出满足 dominoes[i] 和 dominoes[j] 等价的骨牌对 (i, j) 的数量。
示例 1:
- 输入: dominoes = [ [1,2],[2,1],[3,4],[5,6] ]
- 输出: 1
示例 2:
- 输入: dominoes = [ [1,2],[1,2],[1,1],[1,2],[2,2] ]
- 输出: 3
参考代码
| |
主要思路
规范化骨牌顺序:
- 对于每一张骨牌
(a, b),我们通过swap函数确保骨牌的数字以小到大的顺序存储。这样可以将[a, b]和[b, a]归为同一骨牌。
- 对于每一张骨牌
计数骨牌出现次数:
- 使用一个
map来记录每种规范化后的骨牌的出现次数。
- 使用一个
计算等价对的数量:
- 对于每种骨牌,通过组合公式
n * (n - 1) / 2计算出从n张相同骨牌中选出的成对组合。这一公式的意义在于从n项中选择两个的组合。
- 对于每种骨牌,通过组合公式
中等题
11. 盛最多水的容器
给定一个长度为 n 的整数数组 height 。有 n 条垂线,第 i 条线的两个端点是 (i, 0) 和 (i, height[i]) 。
找出其中的两条线,使得它们与 x 轴共同构成的容器可以容纳最多的水。
返回容器可以储存的最大水量。
说明: 你不能倾斜容器。
示例 1:
- 输入: [1,8,6,2,5,4,8,3,7]
- 输出: 49
示例 2:
- 输入: height = [1,1]
- 输出: 1
参考代码
| |
解题思路
双指针法:
- 使用两个指针分别指向数组的两端,逐步向中间移动指针。这样可以在 O(n) 的时间复杂度内解决问题。
容量计算:
- 容器的容量由宽度和高度决定。宽度是两个指针之间的距离,高度是两条线中较短的一条。
- 容量公式为:
capacity = (right - left) * h,其中h = min(height[left], height[right])。
更新最大容量:
- 每次计算当前容量时,跟新记录的最大容量,确保输出的为最大值。
指针移动策略:
- 每次移动指针时,选择高度较小的一边进行移动,这是因为高度的限制将直接影响容量,移动较小的一侧能够寻找可能的更高线,从而增加容量。
581. 最短无序连续子数组
给你一个整数数组 nums ,你需要找出一个 连续子数组 ,如果对这个子数组进行升序排序,那么整个数组都会变为升序排序。请你找出符合题意的 最短 子数组,并输出它的长度。
示例 1:
- 输入: nums = [2,6,4,8,10,9,15]
- 输出: 5
- 解释: 你只需要对 [6, 4, 8, 10, 9] 进行升序排序,那么整个表都会变为升序排序。
示例 2:
- 输入: nums = [1,2,3,4]
- 输出: 0
示例 3:
- 输入: nums = [1]
- 输出: 0
参考代码
| |
关键步骤
边界条件判断:
- 首先检查数组是否只有一个元素,如果是,则无需排序,直接返回 0。
初始化变量:
maxLeft:从左侧开始遍历时已找到的最大值,初始化为数组的第一个元素。minRight:从右侧开始遍历时已找到的最小值,初始化为数组的最后一个元素。left和right:记录无序子数组的左右边界,初始值分别为 0 和数组长度减 1。
查找无序子数组的左边界:
- 从左到右遍历数组:
- 如果当前元素大于等于
maxLeft,更新maxLeft。 - 否则,发生了无序,因此更新左边界
left。
- 如果当前元素大于等于
- 从左到右遍历数组:
查找无序子数组的右边界:
- 从右到左遍历数组:
- 如果当前元素小于等于
minRight,更新minRight。 - 否则,发生了无序,因此更新右边界
right。
- 如果当前元素小于等于
- 从右到左遍历数组:
计算并返回无序子数组的长度:
- 如果
left大于right,则说明找到了无序子数组,返回其长度left - right + 1。 - 否则,表示整个数组已经有序,返回 0。
- 如果
665. 非递减数列
给你一个长度为 n 的整数数组 nums ,请你判断在 最多 改变 1 个元素的情况下,该数组能否变成一个非递减数列。
我们是这样定义一个非递减数列的: 对于数组中任意的 i (0 <= i <= n-2),总满足 nums[i] <= nums[i + 1]。
示例 1:
- 输入: nums = [4,2,3]
- 输出: true
- 解释: 你可以通过把第一个 4 变成 1 来使得它成为一个非递减数列。
示例 2:
- 输入: nums = [4,2,1]
- 输出: false
- 解释: 你不能在只改变一个元素的情况下将其变为非递减数列。
参考代码
| |
代码分析
初始化变量:
- 使用一个计数器
count来统计改变的次数,初始值为0。 - 在数组的开头和结尾分别插入最小值和最大值以方便比较。
- 使用一个计数器
遍历数组:
- 从插入的元素后开始遍历至倒数第二个元素。
- 对于每一个元素,检查其是否满足非递减的条件: - 如果当前元素小于前一个元素或大于后一个元素,则需要处理。
处理不满足条件的情况:
- 检查当前元素与其相邻元素的大小关系,如果当前元素<前一个元素且>后一个元素,返回
false(无法通过变化一个元素满足条件)。 - 如果当前元素小于前一个元素:
- 检查前一个元素与后一个元素的关系,适当改变当前元素或前一个元素,并增加改变计数。
- 之后再检查前两个元素的顺序是否仍然满足条件,如果不满足,则返回
false。
- 如果当前元素大于后一个元素: - 同样地检查当前元素与前后元素的关系,适当改变元素并增加改变计数。
- 检查当前元素与其相邻元素的大小关系,如果当前元素<前一个元素且>后一个元素,返回
改变次数限制:
- 在每次改变后检查
count,如果超过1次则返回false,以满足最多改变一个元素的限制。
- 在每次改变后检查
返回结果:
- 遍历结束后,如果没有超过1次的改变,则返回
true,表示可以通过最少的改变使数组成为非递减数列。
- 遍历结束后,如果没有超过1次的改变,则返回
840. 矩阵的幻方
3 x 3 的幻方是一个填充有 从 1 到 9 的不同数字的 3 x 3 矩阵,其中每行,每列以及两条对角线上的各数之和都相等。
给定一个由整数组成的row x col 的 grid,其中有多少个 3 × 3 的 “幻方” 子矩阵?
注意:虽然幻方只能包含 1 到 9 的数字,但 grid 可以包含最多15的数字。
示例 1:
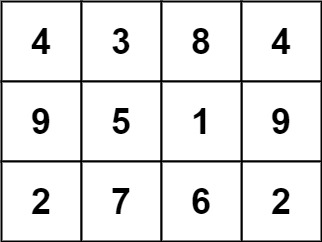
- 输入: grid = [ [4,3,8,4],[9,5,1,9],[2,7,6,2] ]
- 输出: 1
- 解释: 下面的子矩阵是一个 3 x 3 的幻方:
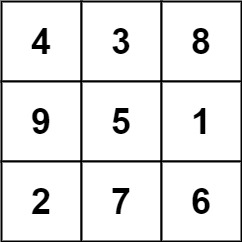
而这一个不是:
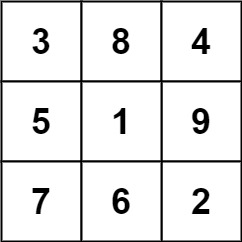
总的来说,在本示例所给定的矩阵中只有一个 3 x 3 的幻方子矩阵。
示例 2:
- 输入: grid = [ [8] ]
- 输出: 0
参考代码
| |
函数步骤
获取网格尺寸:
- 行数
row和列数col通过grid.size()和grid[0].size()获得。
- 行数
边界检查:
- 如果行数或列数小于3,直接返回0,因为无法形成3x3的幻方。
初始化变量:
contrast设置为15,表示每行、列及对角线和应当为15。count用于计数符合条件的幻方个数。
遍历子矩阵:
- 使用双重循环遍历所有可能的3x3子矩阵。
- 创建
flag标记,初始化为true,用于判断当前子矩阵是否合法。 - 创建
nums数组,用于记录1到15的数字出现次数。
检查子矩阵合法性:
- 内嵌循环检查当前3x3子矩阵中的数字:
- 如果数字不在1到9之间或已出现,则标记为不合法(
flag = false)。
- 如果数字不在1到9之间或已出现,则标记为不合法(
- 如果子矩阵不合法,跳过该子矩阵的后续检查。
- 内嵌循环检查当前3x3子矩阵中的数字:
计算和:
- 计算3行、3列和两条对角线的和。
- 检查这些和是否都等于15。
计数符合条件的幻方:
- 如果所有和都等于15,则将
count增加1。
- 如果所有和都等于15,则将
返回结果:
- 最后,返回满足条件的幻方数量
count。
- 最后,返回满足条件的幻方数量
849. 到最近的人的最大距离
给你一个数组 seats 表示一排座位,其中 seats[i] = 1 代表有人坐在第 i 个座位上,seats[i] = 0 代表座位 i 上是空的(下标从 0 开始)。
至少有一个空座位,且至少有一人已经坐在座位上。
亚历克斯希望坐在一个能够使他与离他最近的人之间的距离达到最大化的座位上。
返回他到离他最近的人的最大距离。
示例 1:
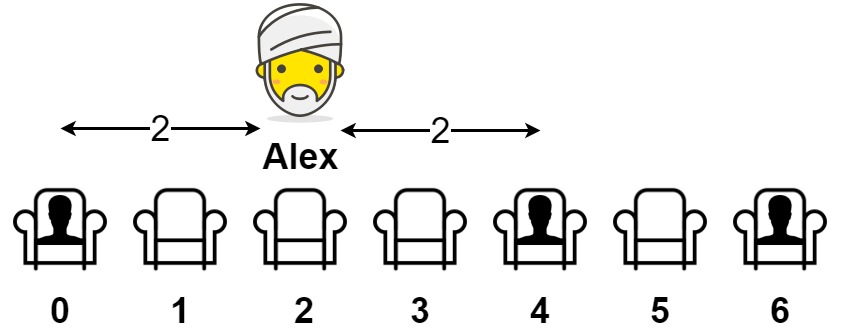
- 输入: seats = [1,0,0,0,1,0,1]
- 输出: 2
- 解释: 如果亚历克斯坐在第二个空位(seats[2])上,他到离他最近的人的距离为 2 。 如果亚历克斯坐在其它任何一个空位上,他到离他最近的人的距离为 1 。 因此,他到离他最近的人的最大距离是 2 。
示例 2:
- 输入: seats = [1,0,0,0]
- 输出: 3
- 解释: 如果亚历克斯坐在最后一个座位上,他离最近的人有 3 个座位远。 这是可能的最大距离,所以答案是 3 。
示例 3:
- 输入: seats = [0,1]
- 输出: 1
参考代码
| |
主要思路
初始化变量:
index: 存储离亚历克斯最近人的位置,用于后续判断。count: 当前连续空座位的计数。leftmaxDistance: 记录左侧最大距离。maxDistance: 记录当前找到的最大距离。
处理边界情况:
- 在数组末尾添加一个
1,这可以方便地处理最后一个人坐的位置的计算,避免边界条件的问题。
- 在数组末尾添加一个
遍历数组:
- 通过循环遍历每个座位,当遇到有人坐的座位 (
seats[i] == 1) 时:- 更新最大距离(
maxDistance)和已坐位置的索引index。 - 如果当前座位的左侧没有人,更新左侧的最大距离。
- 如果当前最大距离与左侧最大距离的关系满足条件,进行更新。
- 处理最后一个人坐的位置的特殊情况。
- 更新最大距离(
- 若当前座位为空 (
seats[i] == 0),则更新空座位计数。
- 通过循环遍历每个座位,当遇到有人坐的座位 (
返回结果:
- 根据
index和maxDistance的值来判断如何返回最终结果,考虑了最大距离的奇偶性。
- 根据
1497. 检查数组对是否可以被 k 整除
给你一个整数数组 arr 和一个整数 k ,其中数组长度是偶数,值为 n 。
现在需要把数组恰好分成 n / 2 对,以使每对数字的和都能够被 k 整除。
如果存在这样的分法,请返回 true ;否则,返回 false。
示例 1:
- 输入: arr = [1,2,3,4,5,10,6,7,8,9], k = 5
- 输出: true
- 解释: 划分后的数字对为 (1,9),(2,8),(3,7),(4,6) 以及 (5,10) 。
示例 2:
- 输入: arr = [1,2,3,4,5,6], k = 7
- 输出: true
- 解释: 划分后的数字对为 (1,6),(2,5) 以及 (3,4) 。
示例 3:
- 输入: arr = [1,2,3,4,5,6], k = 10
- 输出: false
- 解释: 无法在将数组中的数字分为三对的同时满足每对数字和能够被 10 整除的条件。
参考代码
| |
主要步骤
余数记录:
- 使用一个
map<int, int>记录数组中的每个元素与k的余数,并统计每个余数出现的次数。 - 在统计时,如果余数为负,则通过加
k将其转换成非负余数以确保映射的正确性。
- 使用一个
配对检查:
- 遍历余数及其出现次数的映射:
- 如果余数为 0,检查其数量是否为偶数,因为只能成对存在。
- 对于其他余数
m.first,检查当前余数的数量是否等于其对应的余数k - m.first的数量。
- 遍历余数及其出现次数的映射:
返回结果:
- 如果所有条件都满足,返回
true,否则返回false。
- 如果所有条件都满足,返回
LCR 191. 按规则计算统计结果
为了深入了解这些生物群体的生态特征,你们进行了大量的实地观察和数据采集。数组 arrayA 记录了各个生物群体数量数据,其中 arrayA[i] 表示第 i 个生物群体的数量。请返回一个数组 arrayB,该数组为基于数组 arrayA 中的数据计算得出的结果,其中 arrayB[i] 表示将第 i 个生物群体的数量从总体中排除后的其他数量的乘积。
示例 1:
- 输入: arrayA = [2, 4, 6, 8, 10]
- 输出: [1920, 960, 640, 480, 384]
参考代码
| |
关键步骤
初始化:
- 创建一个变量
product用来存储所有非零生物群体数量的乘积。 - 创建一个结果数组
res存储最终结果。 - 创建一个
zeroindex数组记录所有元素为零的索引。
- 创建一个变量
遍历输入数组:
- 如果当前元素为零,将其索引记录到
zeroindex中,并检查零的数量。如果大于1,则直接返回一个全零的数组。 - 如果当前元素非零,则更新
product(乘积)为当前元素的乘积。
- 如果当前元素为零,将其索引记录到
构造结果数组:
- 如果存在零,初始化
res为全零,并将第一个零的位置设置为product(非零乘积)。 - 如果没有零,遍历
arrayA,计算每个元素排除后的乘积,存储在res中(通过将总乘积除以当前元素)。
- 如果存在零,初始化

